递归函数
作者: ryan 发布于: 7/14/2025 更新于: 7/14/2025 字数: 0 字 阅读: 0 分钟
定义
递归是指函数自己调用自己的一种调用方式。
可以分为:
- 直接递归: 函数直接调用自身。
- 间接递归: 通过其他函数间接调用自身(如A调用B,B调用C,C又调用A)。
注意:每一次函数调用都是独立的不相干的。
- 递归一定要有边界条件
- 当边界条件不满足时,递归前进
- 当边界条件满足时,递归返回
递归落盘子称为递归前进 递归撤盘子称为递归返回
费波那契数列的实现
斐波那契数列是以0开头,然后是1,之后依次是前两个数字加在一起,以此类推。 (后一个数字永远是前两个数字相加之和)
如果设F(n) 为该数列的第n项目 那么这句话可以写成如下形式:F(n)=F(n-1)+F(n-2)
F(0) = 0F(1) = 1F(2) = 1F(n)=F(n-1)+F(n-2)
问题:用旧值计算还得用旧值怎么办?
循环实现
思路:
- 使用两个变量
a和b记录前两项,通过循环逐步计算第n项。 - 每次迭代更新
a和b,避免重复计算。
package main
import (
"fmt"
)
func fib(n int) int {
switch { //边界条件处理了负数、0、1和2的特殊情况
case n < 0:
panic("n is negative")
case n == 0:
return 0
case n < 3:
return 1
}
a, b := 1, 1
for i := 0; i < n-2; i++ {
temp := b // 临时存储旧值 b
b = a + b //计算新值:b = F(n+1)
a = temp // 更新 a 为原 b(推进状态)
}
return b // 循环结束后 b=F(n)
}
func main() {
fmt.Println(fib(4))
}使用交换(不支持某些语法的语言就得这么写)需要定义出一个变量来
当i为0,1,2时
i=0 i=1 i=2
temp=1 temp=2 temp=3
b=2 b=3 b=5
a=1 a=2 a=3Go语言支持新的语法,不用再写交换变量。
package main
import (
"fmt"
)
func fibv1(n int) int {
switch { //边界条件处理了负数、0、1和2的特殊情况
case n < 0:
panic("n is negative")
case n == 0:
return 0
case n < 3:
return 1
}
a, b := 1, 1
for i := 0; i < n-2; i++ {
a,b = b, a+b
}
return b // 循环结束后 b=F(n)
}
func main() {
fmt.Println(fib(4))
//执行1->10的结果
for i:=0; i<0; i++ {
fmt.Println(i,fib(i))
}
}#先执行右边
b -> a
a+b -> b
n=3 n=4 n=5 n=6 n=7 n=8
i=0 i=1 i=2 i=3 i=4 i=5
a=1 a=2 a=3 a=5 a=8 a=13
b=2(1+1) b=3(2+1) b=5(2+3) b=8(3+5) b=13(5+8) b=21 (8+13)递归实现
思路:
- 根据递推公式
F(n) = F(n-1) + F(n-2)实现 - 需要边界条件
n=0和n=1。
func fibv1(n int) int {
if n < 0 { panic("n is negative") }
if n == 0 { return 0 }
if n <= 2 { return 1 }
return fib(n-1) + fib(n-2)
}fib(3) 拆分成 fib(2) fib(1) 的返回值相加
循环改递归实现
思路:
- 将循环的迭代过程改为递归调用。
- for的次数变成了函数调用的次数。
- 使用参数传递
a和b,模拟循环中的状态更新。
package main
import "fmt"
func fibv2(n, a, b int) int {
switch {
case n == 0:
return 0
case n < 2:
return b
}
a, b = b, a+b
return fibv2(n-1, a, b)
}
func main() {
fmt.Println(fibv2(3, 1, 1))
}
//if
package main
import "fmt"
func fibv2(n, a, b int) int {
if n == 0 {
return 0
} else if n < 3 {
return b
}
a, b = b, a+b
return fibv2(n-1, a, b)
}
func main() {
fmt.Println(fibv2(3, 1, 1))
}边界反弹壁
每一次递归的调用在做计算,最内层是用来反弹结果的。 递归中 n == 0 或 n < 2 控制递归深度,确保在 n 递减至边界时停止调用

运行效率
以上3个斐波那契数列实现,请问那个效率高?递归效率一定低吗?哪个版本好?
| 实现方式 | 时间复杂度 | 空间复杂度 | 性能表现 |
|---|---|---|---|
fib(迭代) | O(n) | O(1) | ✅ 最优,直接循环计算,无冗余计算 |
fibv1(递归) | O(2ⁿ) | O(n) | ❌ 递归版本1效率极低,是因为有大量重复计算。 |
fibv2(尾递归) | O(n) | O(n) | 递归版本2采用了递归函数调用层次代替循环层次,效率还不错,和循环版效率差不多。 |
fib:约 0.001ms(毫秒级)fibv1:约 10s(秒级)19fibv2:约 0.1ms(受尾调用优化影响较小,但仍优于fibv1)
那么递归版2和循环版谁好?
循环版好些,因为递归有深度限制,再一个函数调用开销较大。
package main
import "fmt"
func fib(n int) int {
switch { //边界条件处理了负数、0、1和2的特殊情况
case n < 0:
panic("n is negative")
case n == 0:
return 0
case n < 3:
return 1
}
a, b := 1, 1
for i := 0; i < n-2; i++ {
temp := b // 临时存储旧值 b b = a + b //计算新值:b = F(n+1)
a = temp // 更新 a 为原 b(推进状态)
}
return b // 循环结束后 b=F(n)
}
func fibv1(n int) int {
if n < 0 {
panic("n is negative")
}
if n == 0 {
return 0
}
if n <= 2 {
return 1
}
return fib(n-1) + fib(n-2)
}
func fibv2(n, a, b int) int {
if n == 0 {
return 0
} else if n < 3 {
return b
}
a, b = b, a+b
return fibv2(n-1, a, b)
}
func main() {
var n = 45
fmt.Println(fib(n))
fmt.Println(fibv2(n, 1, 1))
fmt.Println("~~~~~~~~~~~~~~~")
fmt.Println(fibv1(n))
}第一种使用递归公式为什么慢?
以fib(5)为例。看了下图后,fib(6)是怎样计算的呢?
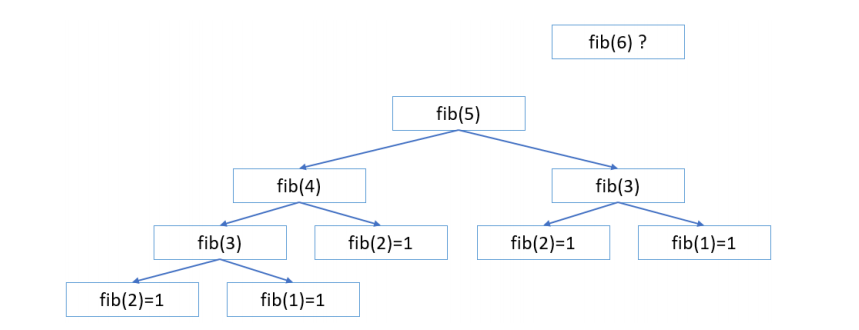
这个函数进行了大量的重复计算,所以慢。
递归要求
Go语言不可能让函数无限调用,递归必须有明确的退出条件,否则会无限调用导致栈溢出(Stack Overflow)。
goroutine stack exceeds 1000000000-byte limit go 保护机制十亿字节
递归调用的深度不宜过深
递归的本质
每次函数调用都会创建一个独立的栈帧(Stack Frame),互不干扰。递归的本质是多次压栈和出栈的过程。
间接递归
间接递归调用,是函数通过别的函数调用了自己,这一样是递归。
package main
func foo() {
bar()
}
func bar() {
foo()
}
func main() {
foo()
}只要是递归调用,不管是直接还是间接,都要注意边界返回问题。但是间接递归调用有时候是非常不明显,代码调用复杂时,很难发现出现了递归调用,这是非常危险的。使用良好的代码规范来避免这种递归的发生。
总结
- 递归是一种很自然的表达,符合逻辑思维
- 递归相对运行效率低,每一次调用函数都要开辟栈帧
- 递归有深度限制,如果递归层次太深,函数连续压栈,栈内存就可能溢出了
- 如果是有限次数的递归,可以使用递归调用,或者使用循环代替,循环代码稍微复杂一些,但是只要不是死循环,可以多次迭代直至算出结果
- 绝大多数递归,都可以使用循环实现
- 即使递归代码很简洁,但是能不用则不用递归
